Projects
This page contains a brief overview of projects that I significantly shaped throughout the entire project life cycle. In academic terms, this mostly corresponds to first-author publications (single and shared). If you’re interested in a full list of projects I have been involved in, please check out my CV.
Consistency Model Posterior Estimation
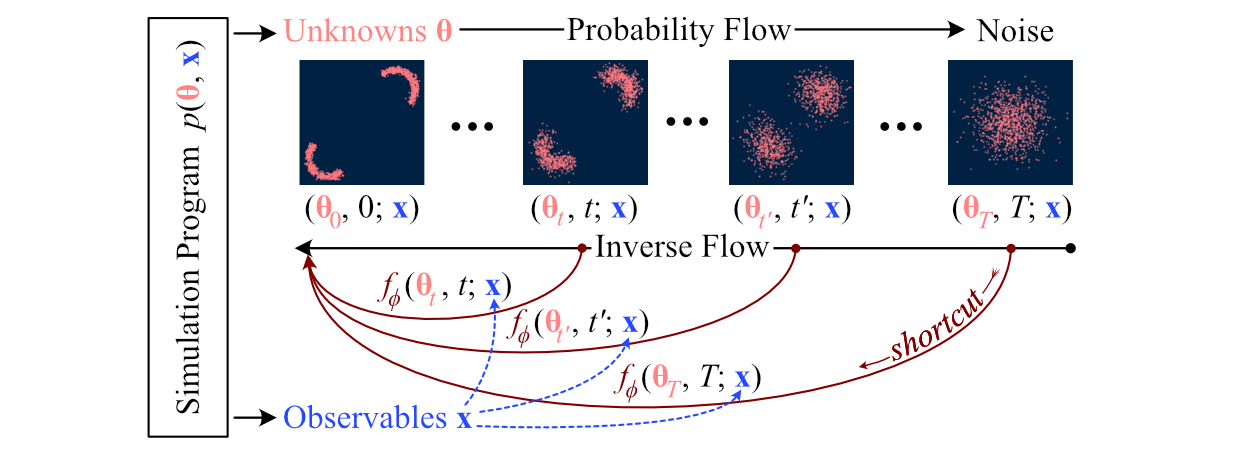
Consistency models for neural posterior estimation (CMPE) is a new free-form conditional sampler for scalable, fast, and amortized simulation-based inference with generative neural networks. CMPE combines the advantages of normalizing flows and flow matching methods into a single generative architecture: It essentially distills a continuous probability flow and enables rapid few-shot inference with an unconstrained architecture that can be tailored to the structure of the estimation problem.
Deep Fusion for Multimodal Simulation-Based Inference
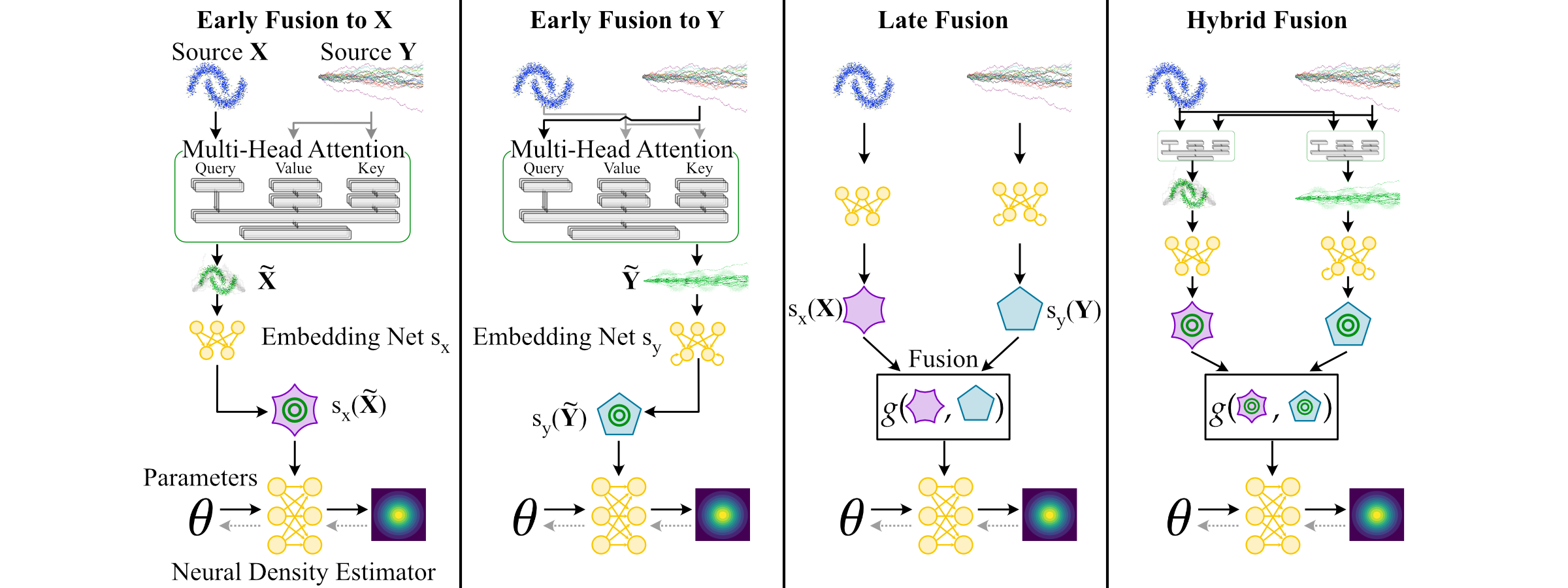
We present multimodal neural posterior estimation (MultiNPE), a method to integrate heterogeneous data from different sources in simulation-based inference with neural networks. Inspired by advances in attention-based deep fusion learning, it empowers researchers to analyze data from different domains and infer the parameters of complex mathematical models with increased accuracy and better performance under partially missing data.
Data-Efficient Amortized Bayesian Inference via Self-Consistency Losses
Short Paper (NeurIPS UniReps 2023)
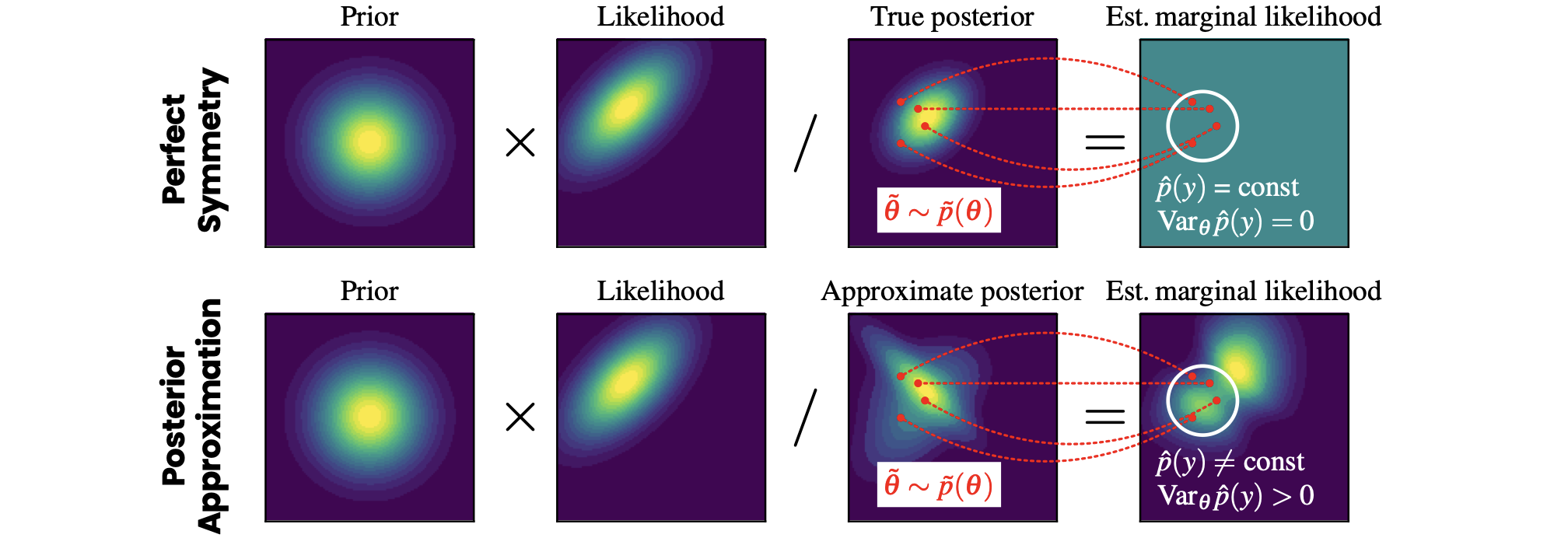
We propose a method to improve the efficiency and accuracy of amortized Bayesian inference by leveraging universal symmetries in the probabilistic joint model \(p(\theta,y)\). In a nutshell, we invert Bayes’ theorem and estimate the marginal likelihood based on approximate representations of the joint model. Upon perfect approximation, the marginal likelihood is constant across all parameter values by definition. However, approximation error leads to undesirable variance in the marginal likelihood estimates across different parameter values. We formulate violations of this symmetry as a loss function to accelerate the learning dynamics of conditional neural density estimators.
Meta-Uncertainty in Bayesian Model Comparison
Paper (AISTATS 2023) | Code | Project website | Poster | Presentation (15min)
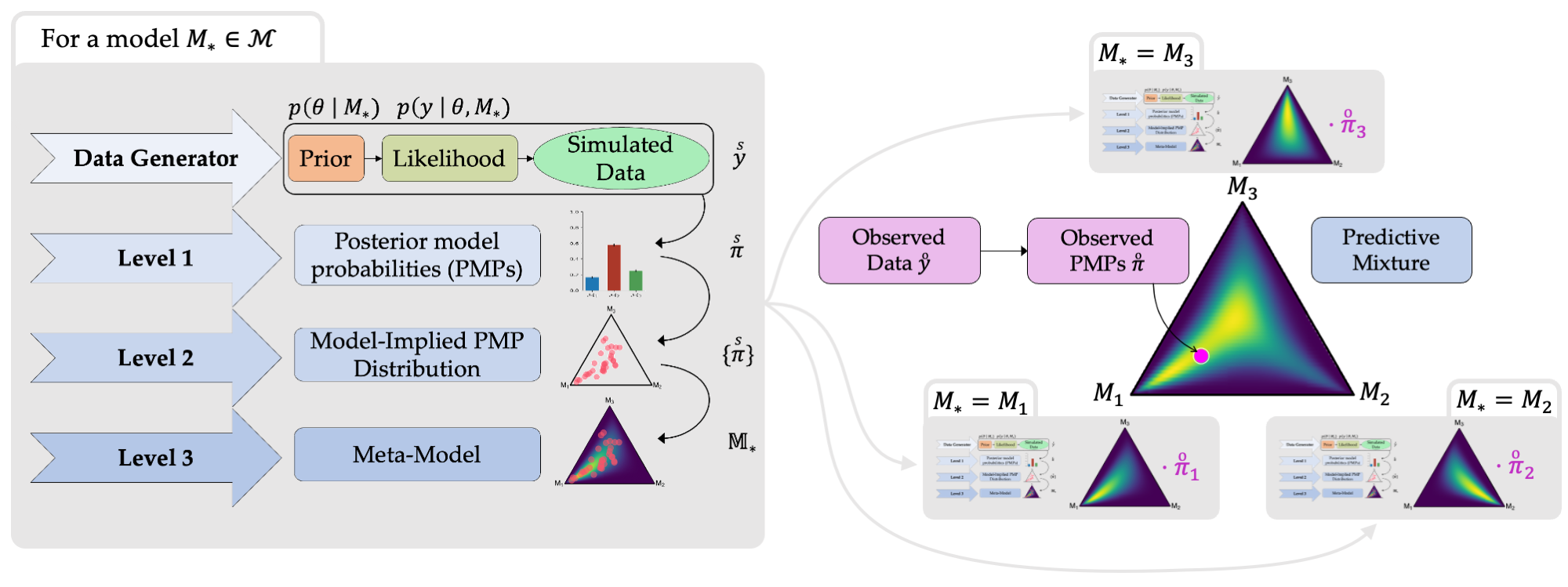
Meta-Uncertainty represents a fully probabilistic framework for quantifying the uncertainty over Bayesian posterior model probabilities (PMPs) using meta-models. Meta-models integrate simulated and observed data into a predictive distribution for new PMPs and help reduce overconfidence and estimate the PMPs in future replication studies.
BayesFlow: Amortized Bayesian Workflows With Neural Networks
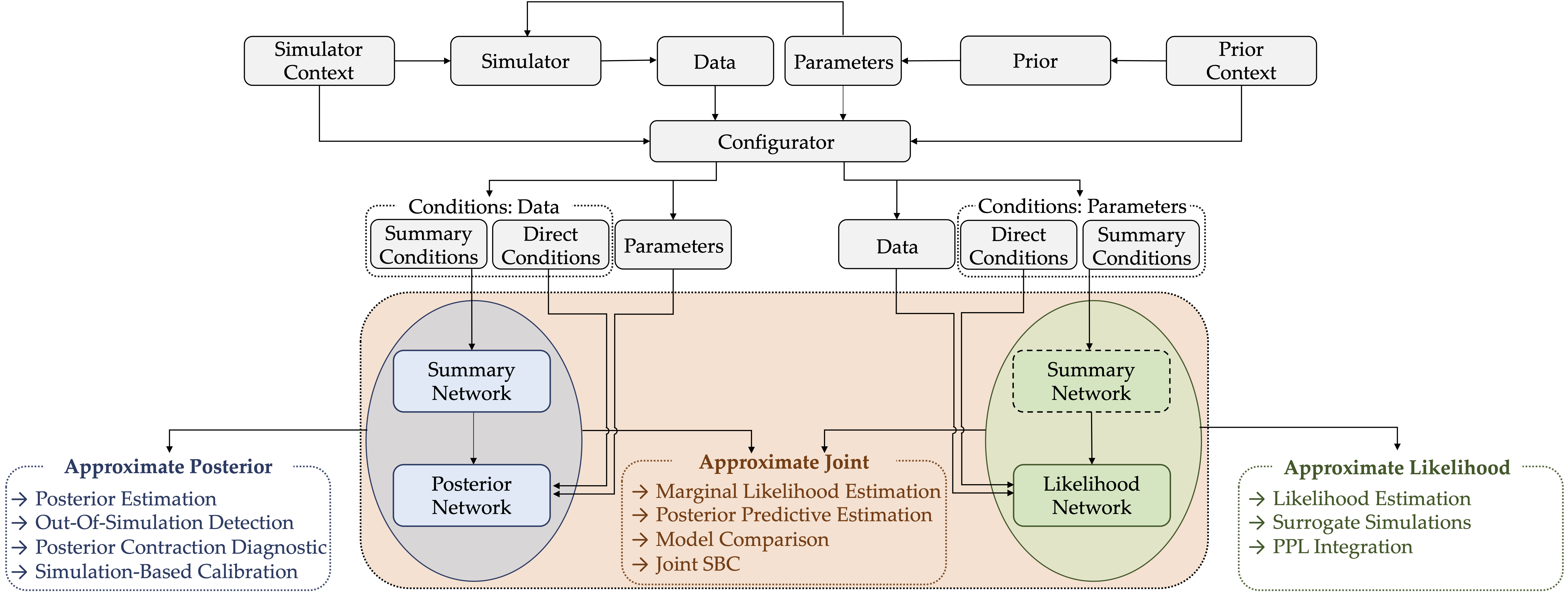
Software Paper | Documentation | BayesFlow Forums (new!)
BayesFlow is a Python library for simulation-based training of established neural network architectures for amortized data compression and inference. Amortized Bayesian inference, as implemented in BayesFlow, enables users to train custom neural networks on model simulations and re-use these networks for any subsequent application of the models. Since the trained networks can perform inference almost instantaneously, the upfront neural network training is quickly amortized.
JANA: Jointly Amortized Neural Approximation of Complex Bayesian Models
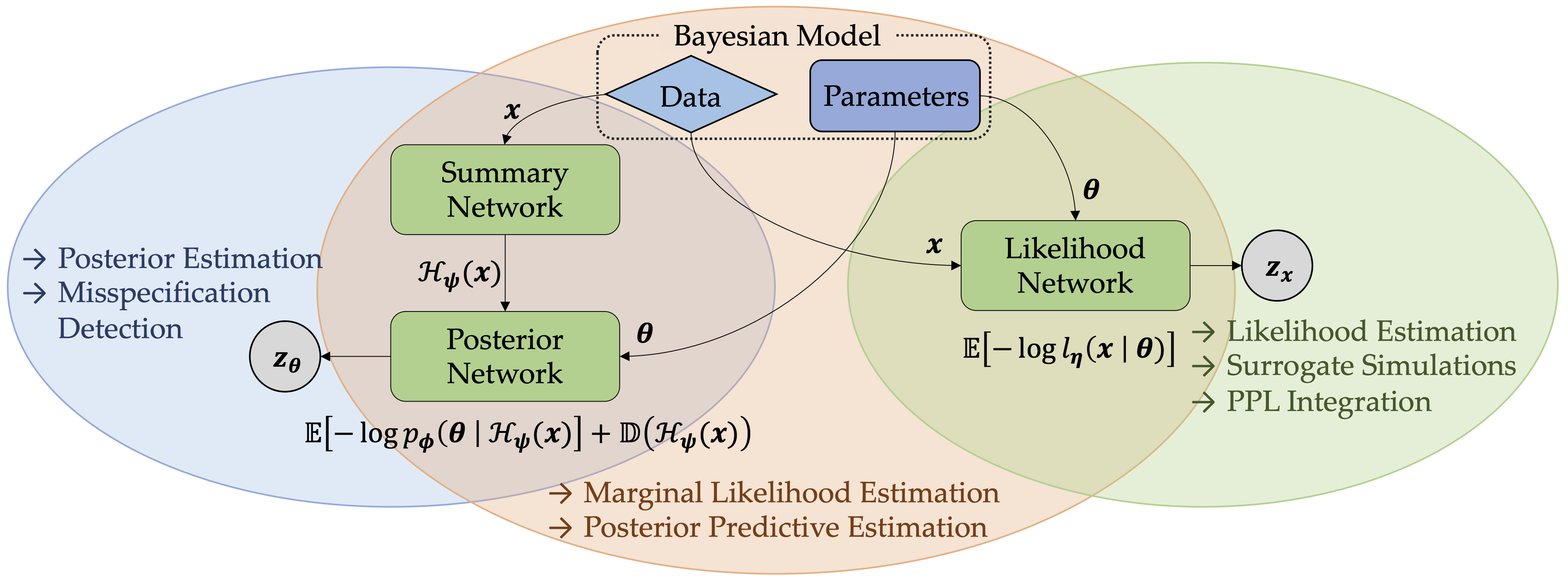
Paper (UAI 2023) | Python library
JANA is a new amortized solution for intractable likelihood functions and posterior densities in Bayesian modeling. It trains three networks to learn both an approximate posterior and a surrogate model for the likelihood, enabling amortized marginal likelihood and posterior predictive estimation.
Detecting Model Misspecification in Amortized Bayesian Inference with Neural Networks
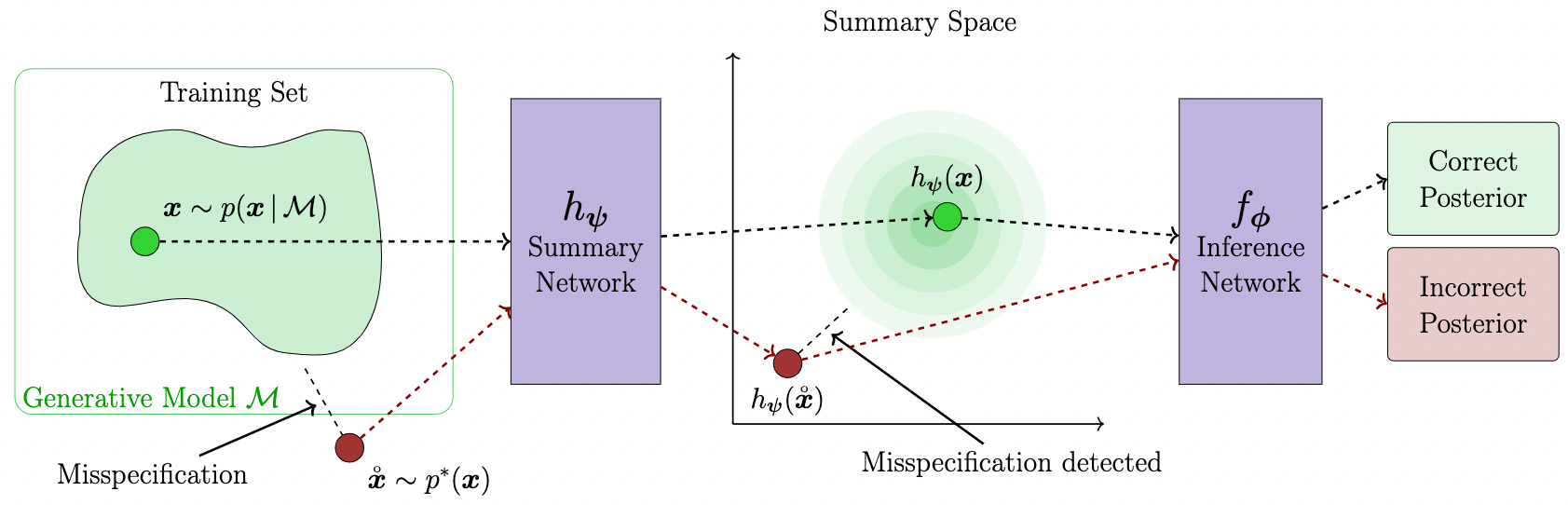
Paper (GCPR 2023, Best Paper Honorable Mention) | Code | Poster
Novel neural network based architectures enable amortized Bayesian inference in settings where the likelihood function is only implicitly defined by a simulation program. But how faithful is such inference when simulations represent reality somewhat inaccurately? This paper illustrates how imposing a probabilistic structure on the latent data summary space can help to detect potentially catastrophic domain shifts during inference.